词法分析
比较简单,不多说了。
语法分析
自顶向下分析方法
构造文法的预测分析程序
例题: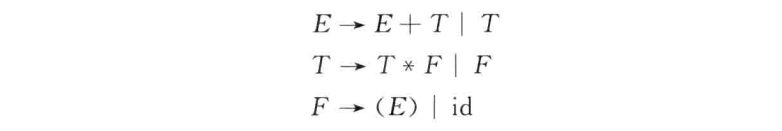
改写文法,消除左递归
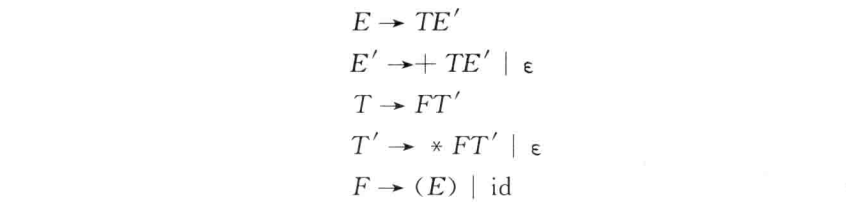
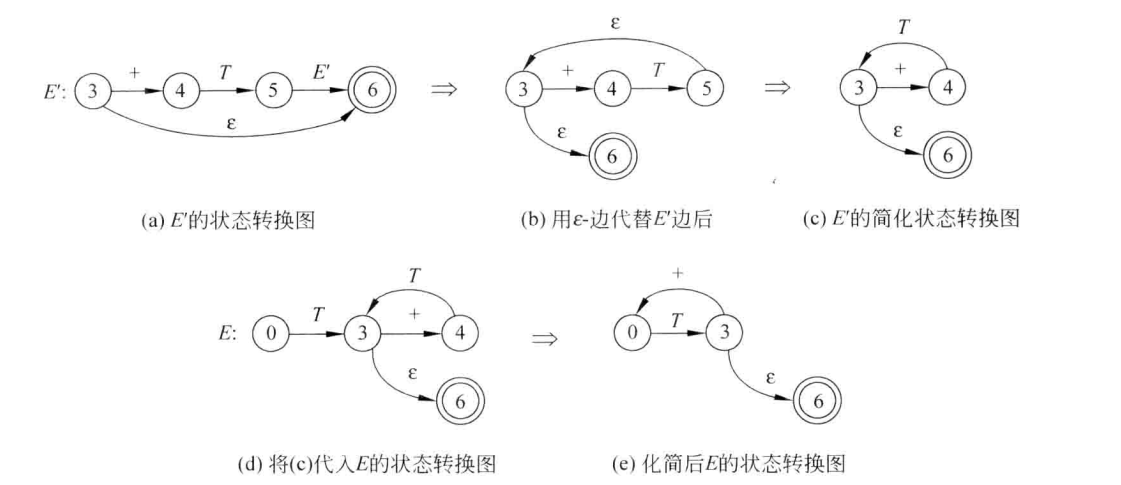
根据改写后的文法,构造状态转换图
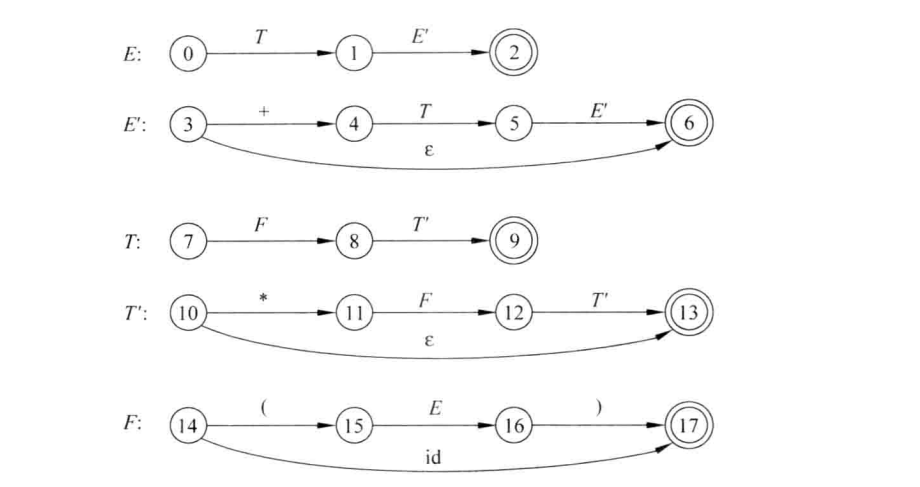
化简状态转换图
真的很奇妙,不是吗
同理得
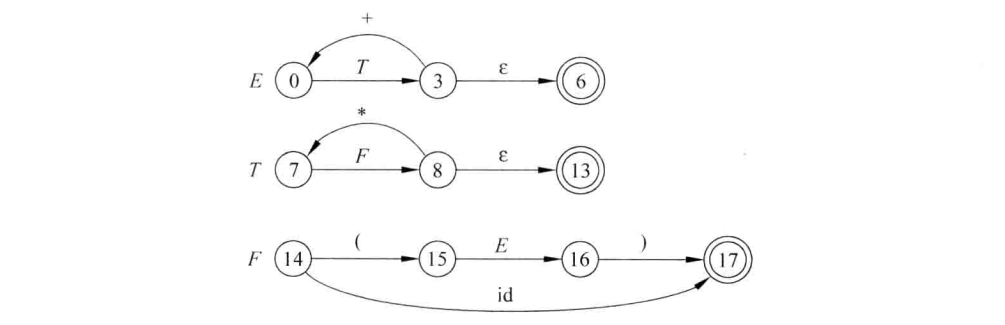
根据化简后的转换图构造程序(注意指针移动)

非递归预测分析
预测分析表的构造
FIRST(X)
定义:X可以推导出的开头终结符号集合
构造方法:
$X$为终结符,则$FIRST(X) = {X}$
$X$为非终结符,且有产生式$X→a…$,其中a为终结符,则$a∈FIRST(X)$
若有产生式$X→ε$,则$ε∈FIRST(X)$
若有产生式$X→Y…$,且Y为非终结符,则将$FIRST(Y)$中的所有非$ε$元素加入$FIRST(X)$
若有产生式$X→Y_1 Y_2…Y_k$,如果对某个$i$,$FIRST(Y_1),FIRST(Y_2),…,FIRST(Y_{i-1})$都含有$ε$,则把$FIRST(Y_i)$中的所有非$ε$元素加入$FIRST(X)$中
若所有的$FIRST(Y_i)$均含有$ε$,则将$ε$加入$FIRST(X)$
FOLLOW(A)
定义:文法的所有句型中紧跟在A之后出现的终结符号或$组成的集合
构造方法:
- 文法开始符号$S$,$∈FOLLOW(S)
- 若有产生式$A→αBβ$,则把$FIRST(β)$中的所有非$ε$元素加入$FOLLOW(B)$
- 若有产生式$A→αB$,或$A→αBβ$但$ε∈FIRST(β)$,则把$FOLLOW(A)$中的所有元素加入$FOLLOW(B)$
构造预测分析表

如果一个文法的预测分析表不含多重定义的表项,则称该文法为$LL(1)$文法

例:预测分析程序的分析过程
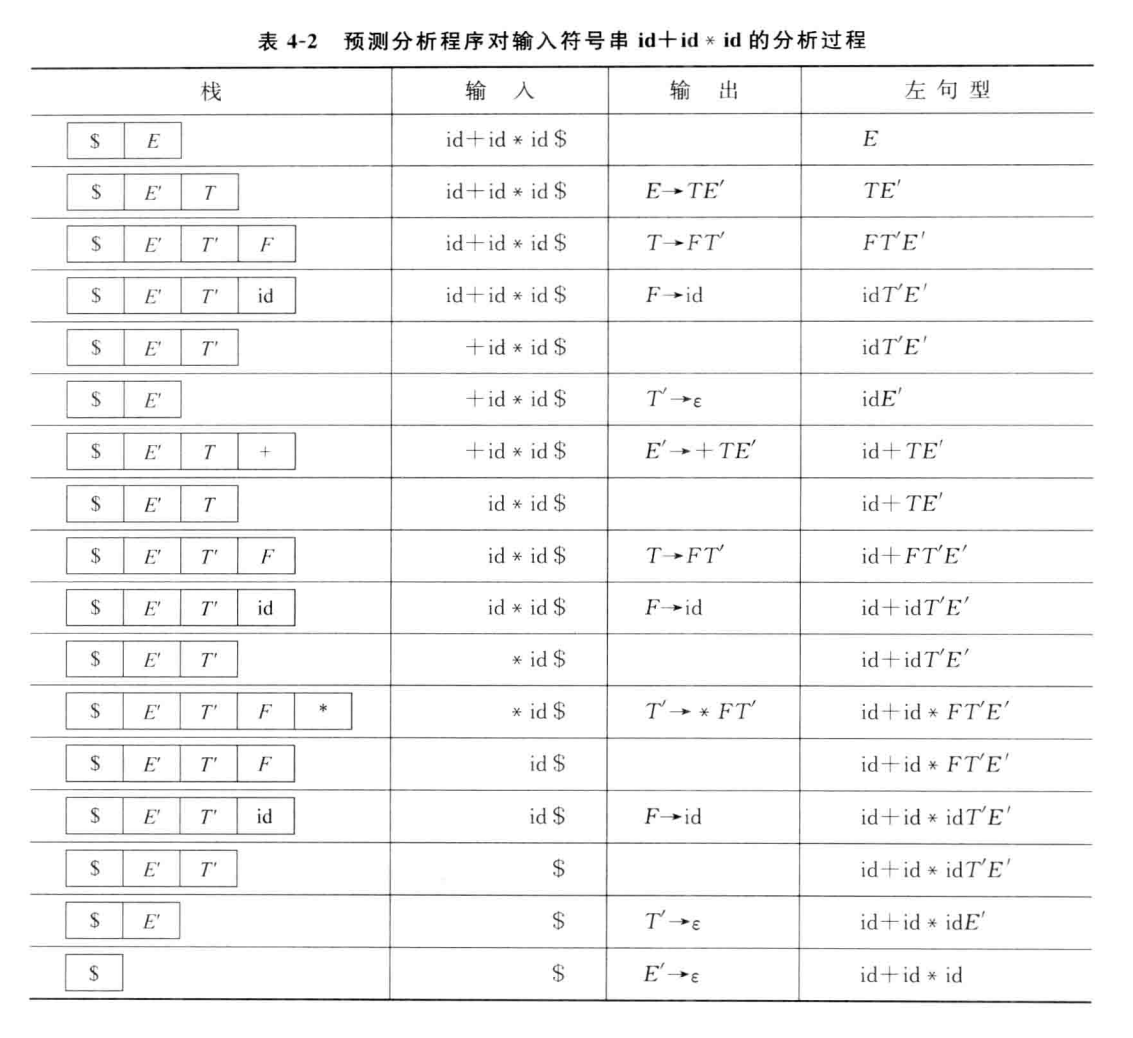
栈中的表达式要倒着写(左边为栈底,右边为栈顶)
匹配时则将栈顶元素出栈,开始匹配输入表达式中下一个符号
错误处理
对非终结符$A$,终结符号$b∈FOLLOW(A)$,如果表项$M[A,b]$为空,则填入$synch$
预测分析程序

自底向上分析方法
LR
分析过程

SLR(1)分析表

构造LR(0)项目集规范族
例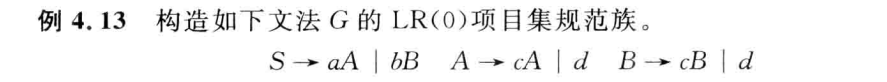

依次构造从$I_i$出发的有效项目集,直到没有新的有效项目集出现。
构造DFA
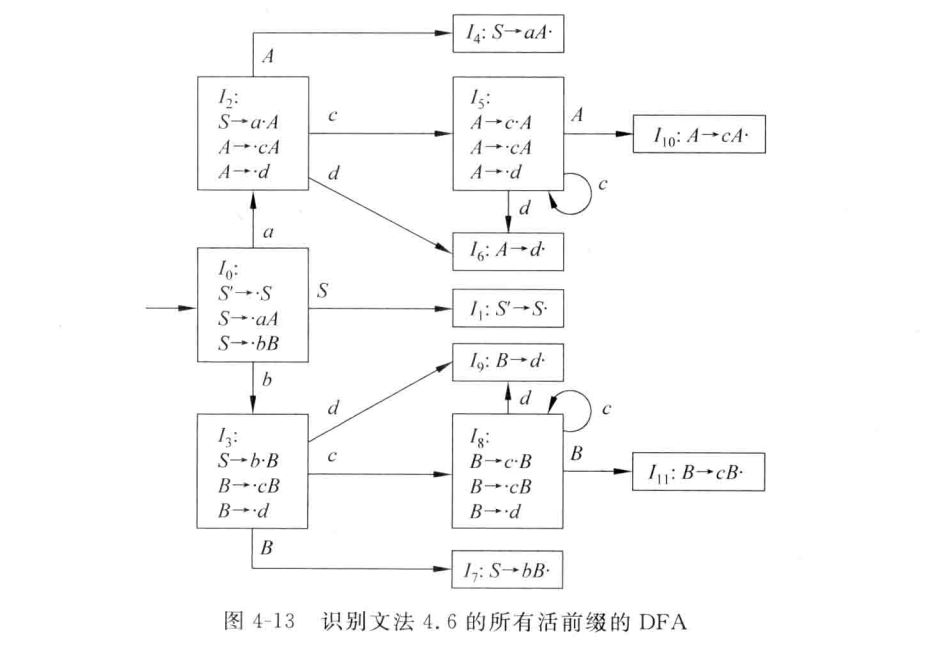
构造SLR(1)分析表
LR(0)可能会产生移进-规约冲突或者规约-规约冲突,SLR(1)考察非终结符号的FOLLOW集

LR(1)分析表
书上的概念看不懂,所以直接看例题。

首先还是构造拓广文法(这里已经给出)
构造项目集时要多向后看一位,用逗号隔开写在后面,由某个式子推导出的项目集继承原式子多看一位的符号(?有点啰嗦ww
展望符计算方法:方法
$FIRST(βa)$ ,其中$β$为原式子该非终结符之后的剩余串,$a$为上个状态的展望符
然后构造分析表
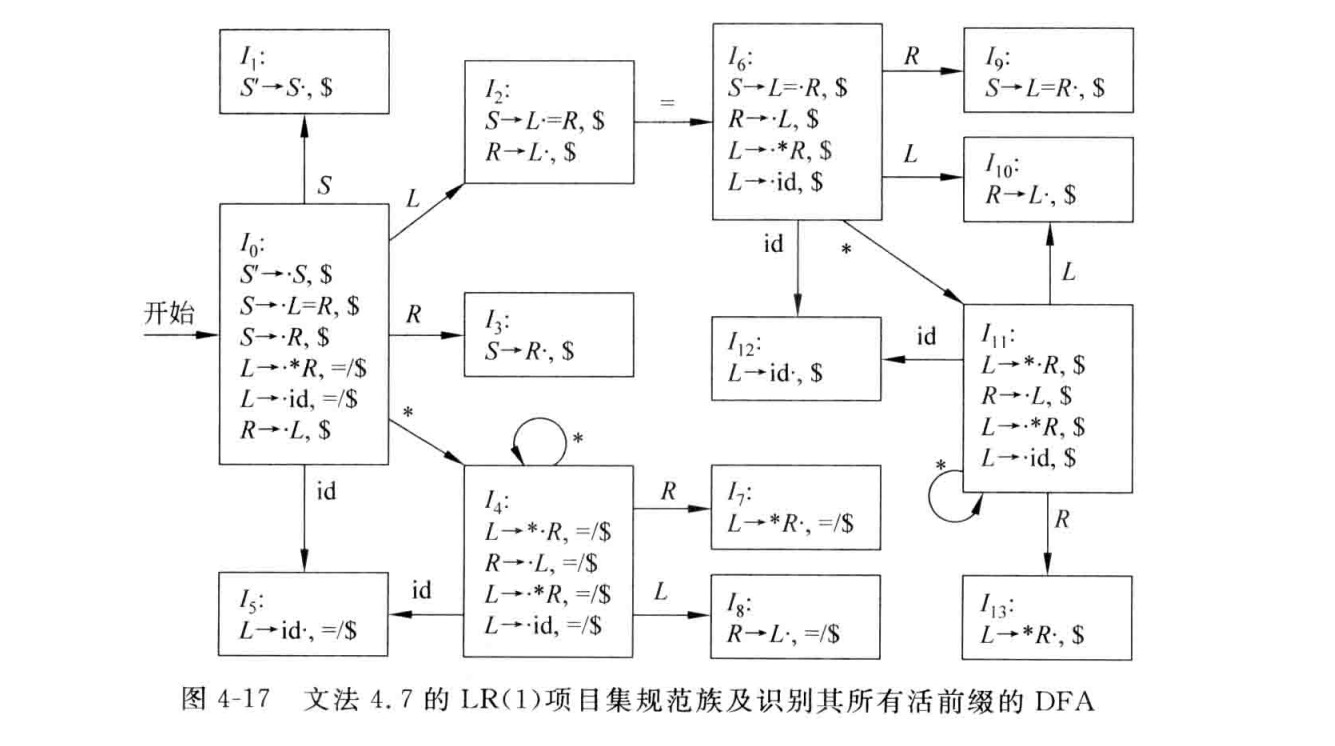
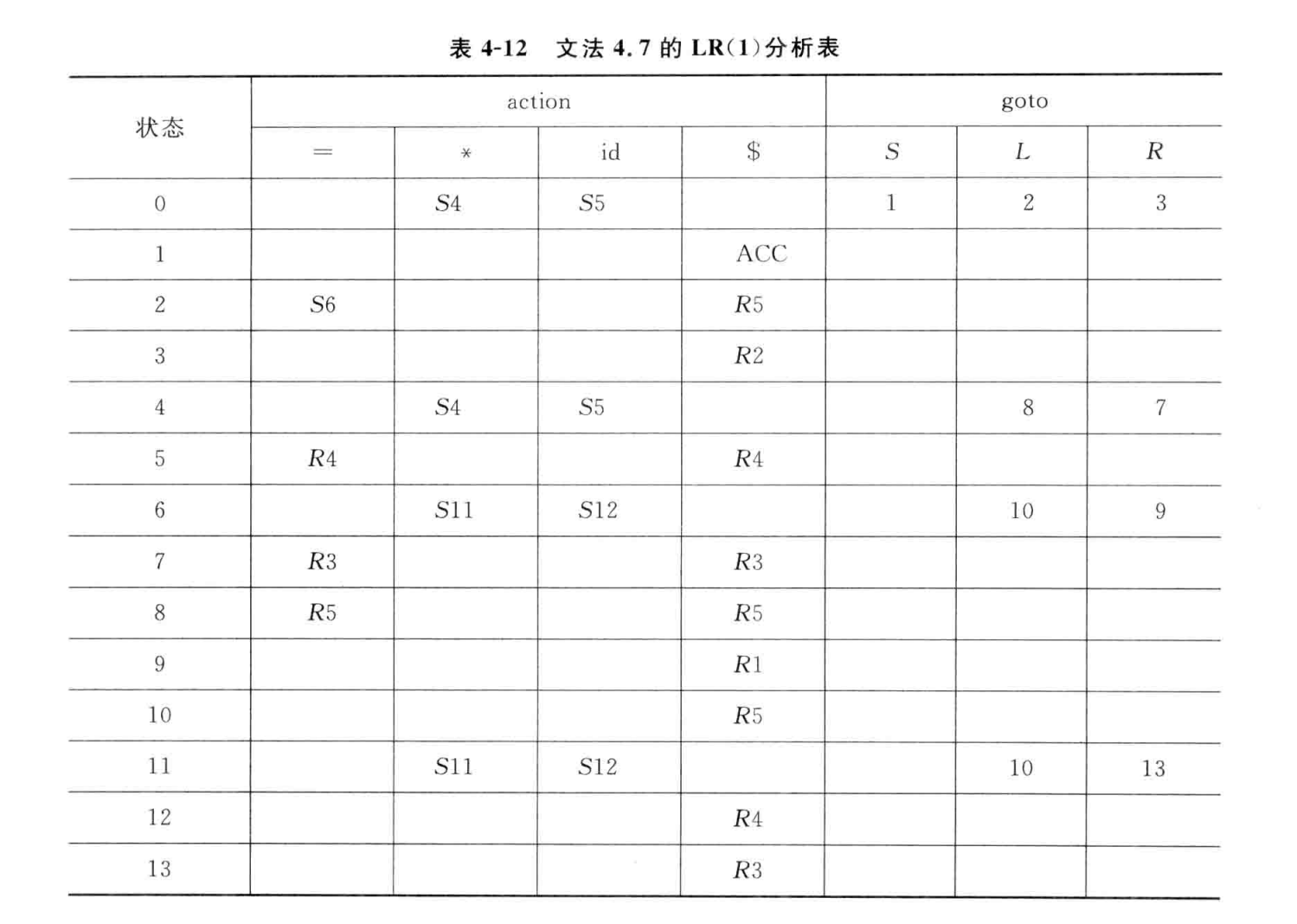
LALR(1)分析表
基本思想
①合并LR(1)项目集规范族中的同心集,以减少分析表的状态数
②用项目集的核代替项目集,以减少项目集所需的存储空间

判断文法
$LR(0)$
一个文法是$LR(0)$文法 当且仅当 该文法的每个活前缀的有效项目集中,要么所有的元素都是移进或待约项目,要么只含有唯一的归约项目。
$SLR(1)$ 和 $LR(1)$

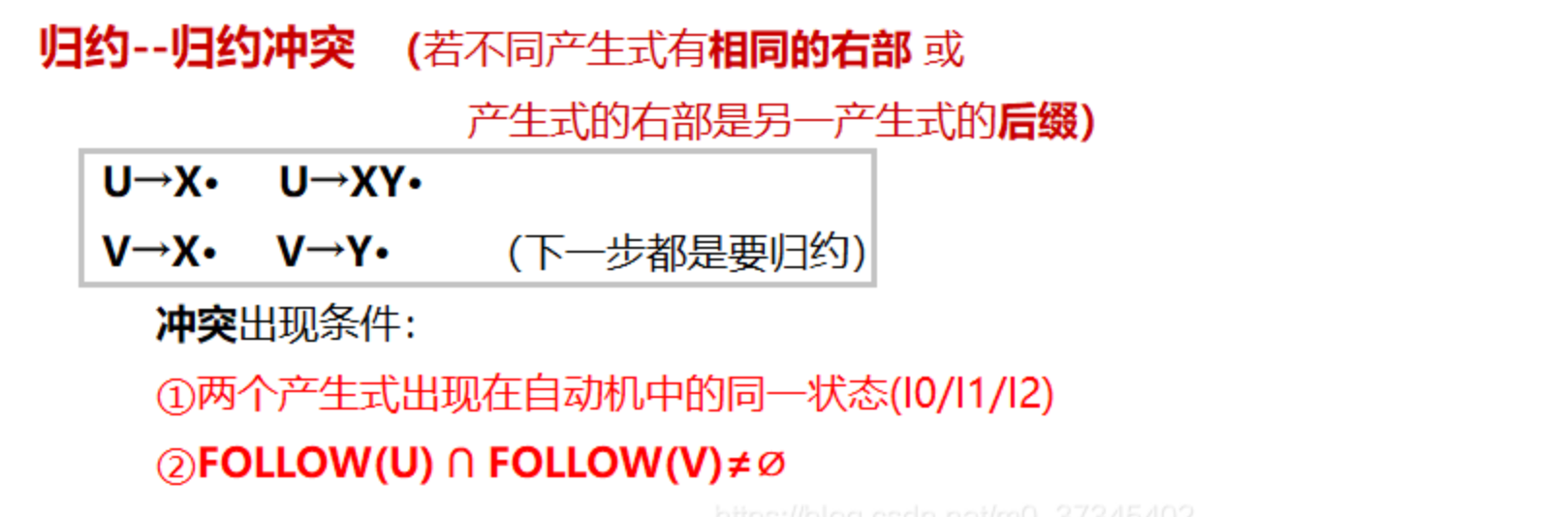
移进-规约冲突
规约-规约冲突

语法制导翻译
学艺不精,没学懂……
语义分析
类型检查
类型表达式
数组
$array(I,T)$
元素类型为T,下标集合为I的数组
例:
a:array[1…10] of char;
名字a的类型表达式为array(1…10, char)
笛卡尔乘积
$T_1×T_2$
记录
把类型构造器record作用于记录中各域类型的笛卡尔乘积上就形成了记录的类型表达式,域类型是由域名和域的类型表达式组成的二元组
例:
B : record
i : integer;
c : char;
r : real;
end;
B的类型表达式为record((i×integer)×(c×char)×(r×real))
与此功能相同的C语言的声明语句为:
struct B{
int i;
char c;
float r;
}
指针
如果T是类型表达式,那么pointer(T)也是类型表达式
例:
p: ↑row;
p的类型表达式为pointer(row)
函数
把程序中的函数看成是从定义域类型D到值域R的映射,函数类型由类型表达式$D→R$表示
例:
function fun(a : char, b : integer): ↑integer;
fun的类型表达式为char × integer → pointer(integer)
类型等价
结构等价
如果两个数据类型具有相同的结构,即都是从相同的基本类型出发、用相同的类型构造器由完全相同的方法构造出来的,那它们就是等价的。
名字等价
名字等价把每个类型名看成一个可区别的类型,所以两个类型表达式名字等价,当且仅当它们的名字完全相同。
C语言的类型等价
C语言对struct和union采用名字等价,其他采用结构等价。
运行环境
非局部名字的访问
静态作用域
活动记录、访问链、display表
动态作用域
活动记录的访问链总是指向它的调用者的活动记录
参数传递机制
建议看作业题7.2,结合答案的图看。
传值调用
函数调用不会改变原来参数的值(即函数外的值仍旧保持不变)。
引用调用
传地址。
通过形参访问参数的地址空间,会改变值。
复制恢复
返回时,传入参数为左值,函数内结果为右值(相当于复制结果)。
传名调用
直接把参数名字传进去,牵一发而动全身。
中间代码生成
中间代码形式
后缀表达式、三地址代码、四元式、三元式
后缀表达式
方法一
运算对象顺序相同,运算符紧跟在其运算对象之后
运算符优先级:括号>算术运算符>关系运算符>逻辑运算符
方法二
设置一个运算符号栈,通过进栈出栈的方式
要注意-是减号还是uminus
三地址代码
一般形式:x := y op z





四元式
(op, arg1, arg2, result)
三元式
在四元式基础上,不引入临时变量,用计算中间结果的语句的序号代替临时变量
赋值语句的翻译

数组
一维数组

二维数组


布尔表达式的翻译
运算符优先级:not > and > or
数值表示法
采用数值编码表示逻辑真和逻辑假。
控制流表示法
利用控制到达程序中的位置表示布尔表达式的真值。
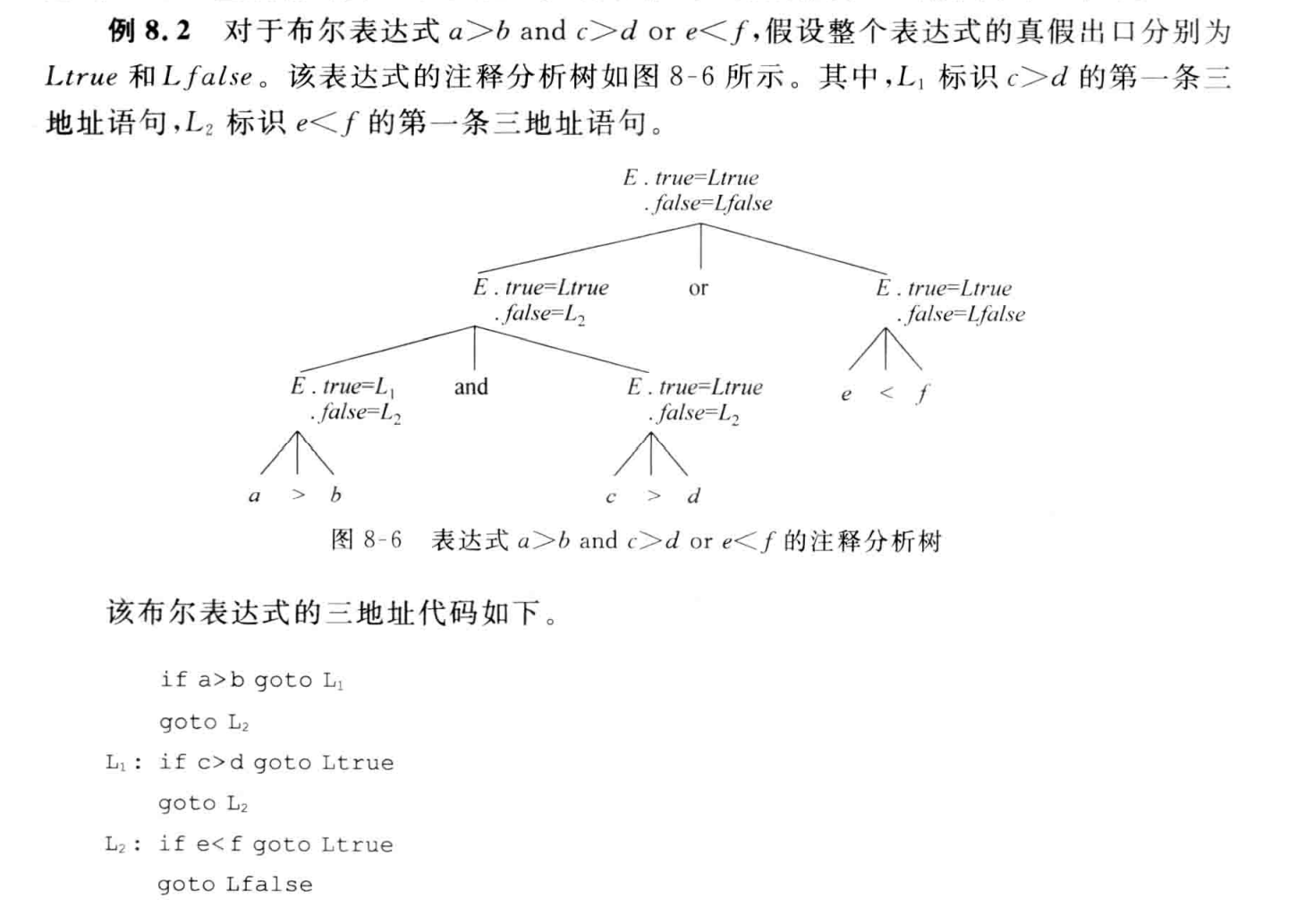
回填技术
把转移到某目标的所有待回填语句的标号都存入一个链表。