听说要考试了,就想着来个系统性的梳理。
语言及文法
语言的定义及运算
简单罗列一下,具体的自己翻书。
字母表,句子(字符串),字符串的长度$|w|$,空串ε
字符串的连接,$εw = wε = w$
字符串的逆$\tilde{w}$是字符串$w$的倒置
前缀、后缀、子串,空串是任何字符串的前缀、后缀及子串
$T^*$表示字母表T上所有字符串和空串的集合,$T^+$是字母表T上所有字符串构成的集合
字母表T上的语言
语言$L_1$、$L_2$的积$L_1L_2$是由$L_1$、$L_2$中字符串连接所构成的字符串的集合
语言$L$的幂、闭包、正闭包
文法的定义

文法的分类
愣着干嘛,背下来啊……
0型
对生成式的形式不加任何限制,产生的语言:无限制性语言
1型
上下文有关文法,产生的语言:上下文有关语言
生成式形式为:$α→β$,其中$|α| ≤ |β|$,且$α、β∈( N ∪ T)^+$,且$α$至少有一个非终结符号
1型文法每个生成式左部字符串长度小于或等于右部字符串长度。
例:
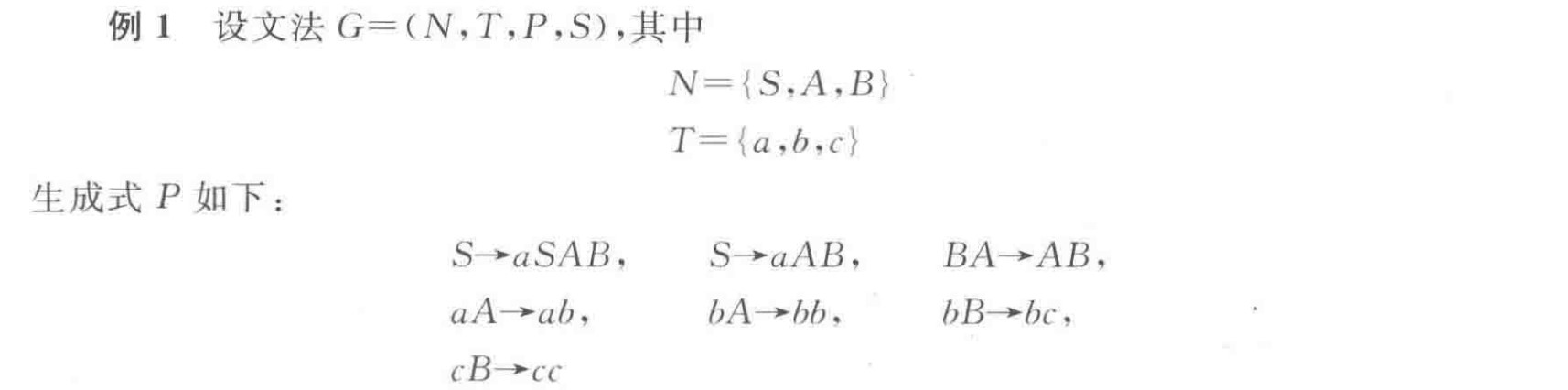
2型
上下文无关文法,产生的语言:上下文无关语言
生成式形式为:$A→α$,$A∈N$且$α∈(N∪T)^*$
2型文法每个生成式左部是单个非终结符。
例:
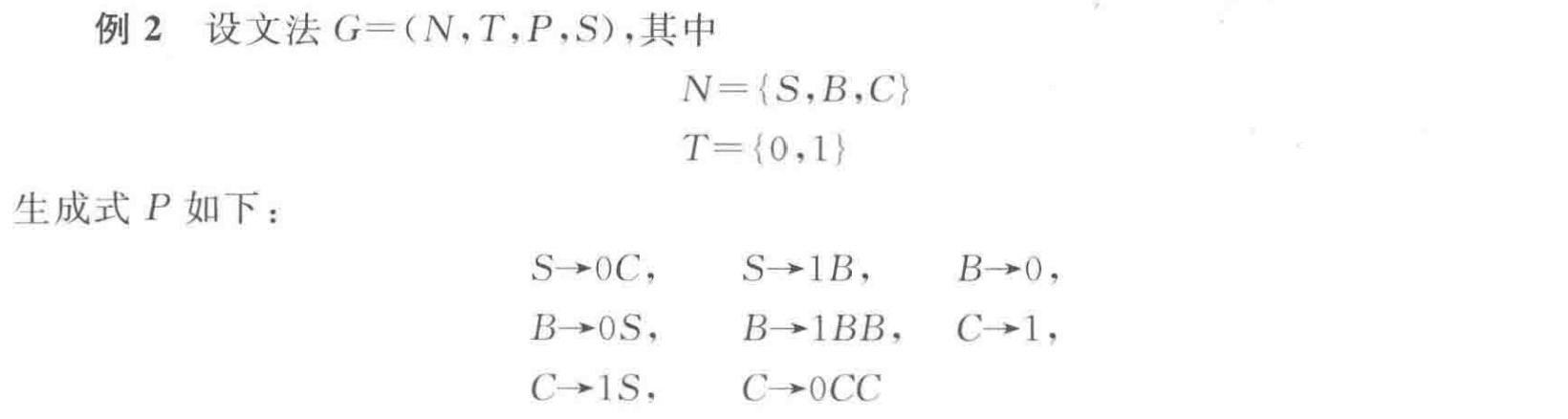
3型
正则文法,产生的语言:正则语言
右线性文法:$A→wB$或$A→w$,$A、B∈N$,$w∈T^*$
左线性文法:$A→Bw$或$A→w$,$A、B∈N$,$w∈T^*$
例:
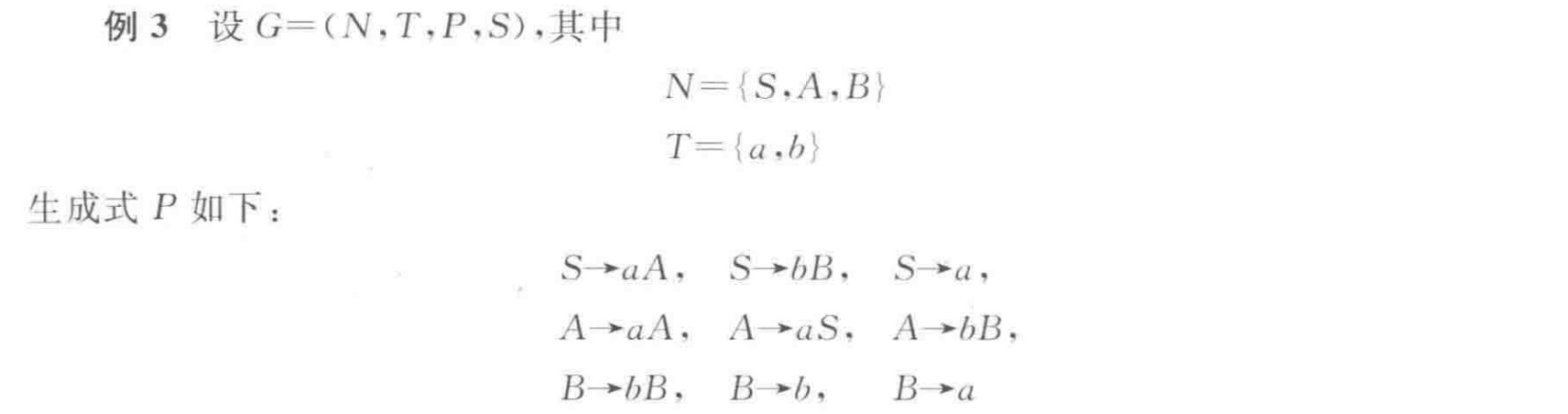
有限自动机和右线性文法
NFA转换为DFA
子集构造法
例:
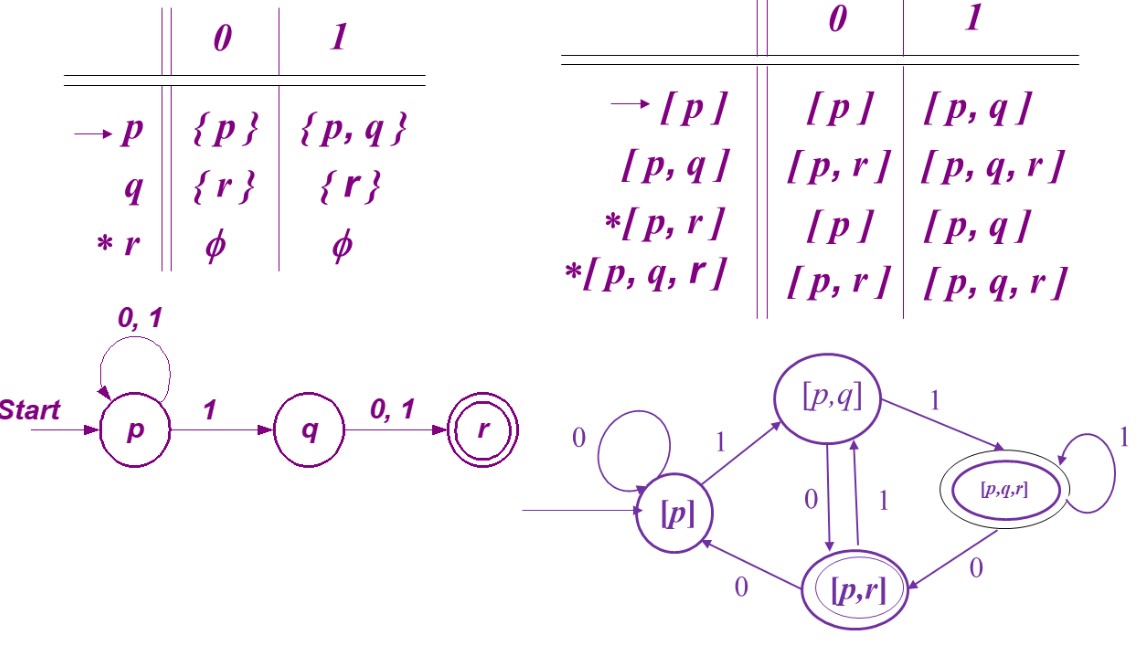
不会吧不会吧,不会写完实验一还不会子集构造法吧。
ε-closure
从已知状态$q$仅用$ε$转换就可以到达的状态集合(包括$q$自身)。
状态子集的$ε$-闭包是子集中各状态的$ε$-闭包的并。
ε-NFA转换为NFA
从状态$p$接收字符$a$转移到状态$q$,状态$q$接收$ε$可以到达状态$r$,则生成的NFA中状态$p$接收字符$a$可以到达状态$q$和状态$r$。即状态$p$接收字符$a$可以到达状态$q$的ε-closure。
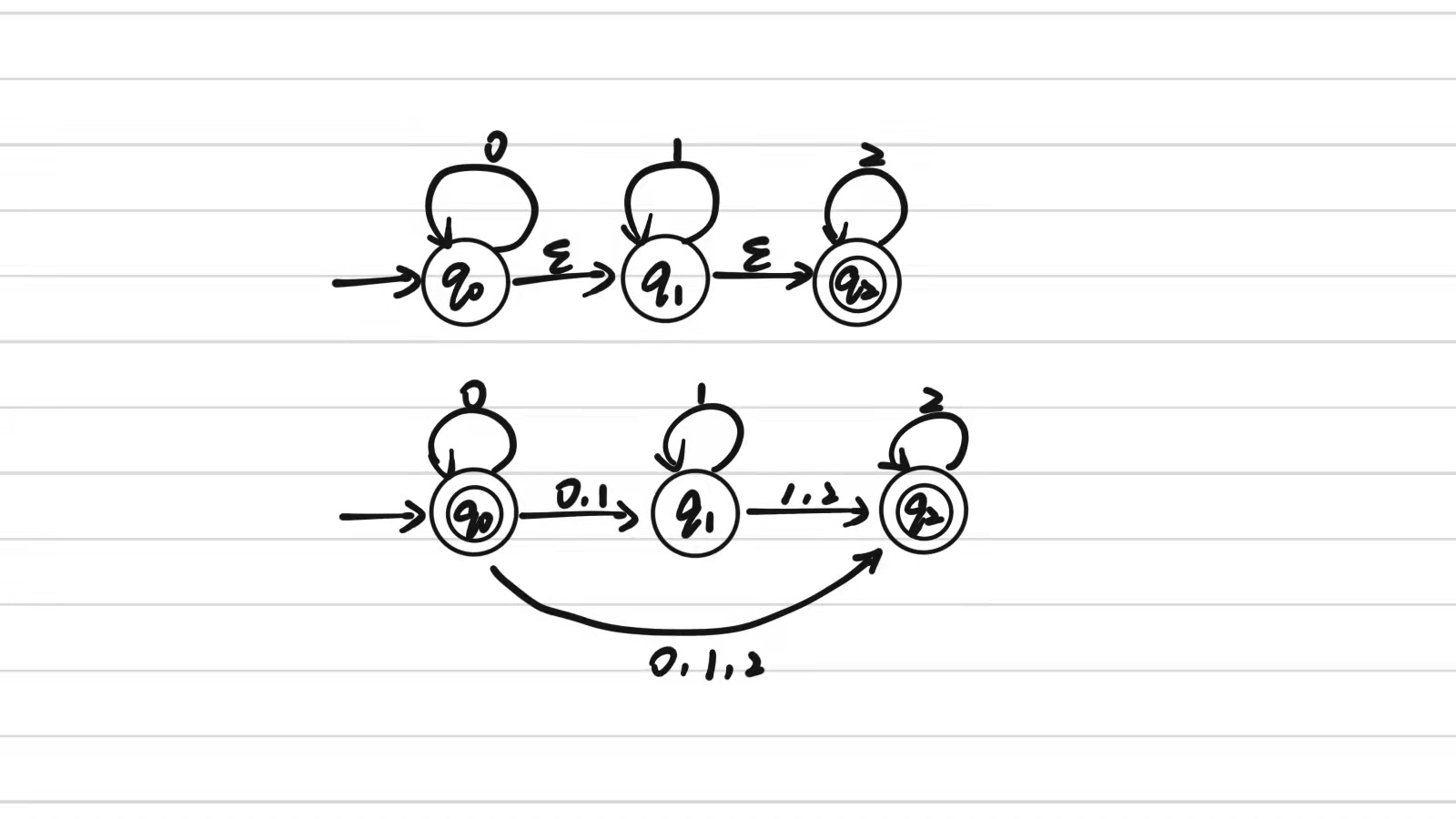
正则集与正则式

一个正则集至少对应一个正则式。
一个正则式只对应一个正则集。(两个正则式表示相同的正则集,则这两个正则式相等)

规则R
$设x = αx + β,α∈$$T^*$$,β∈$$(N∪T)^*$$,x∈N,其解x = α^*β。$
这个真的非常好用!背住了以后有手就行。
例:
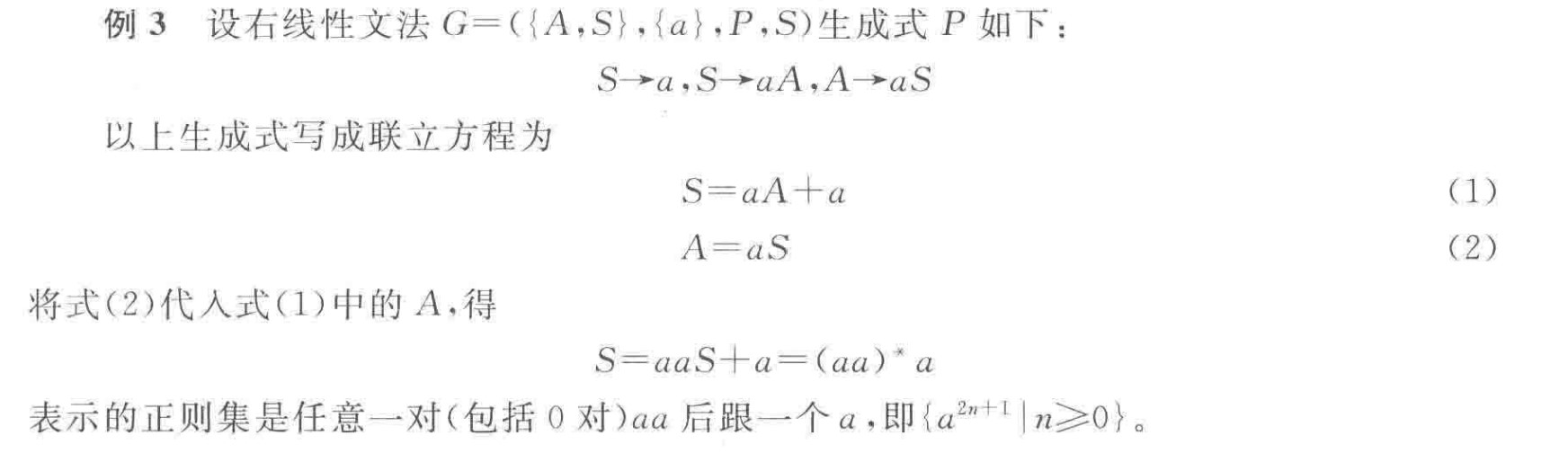
右线性文法和正则集
一个语言是正则集$\iff$该语言为右线性文法
正则表达式和有限自动机
DFA构造正则表达式
中间状态消去法
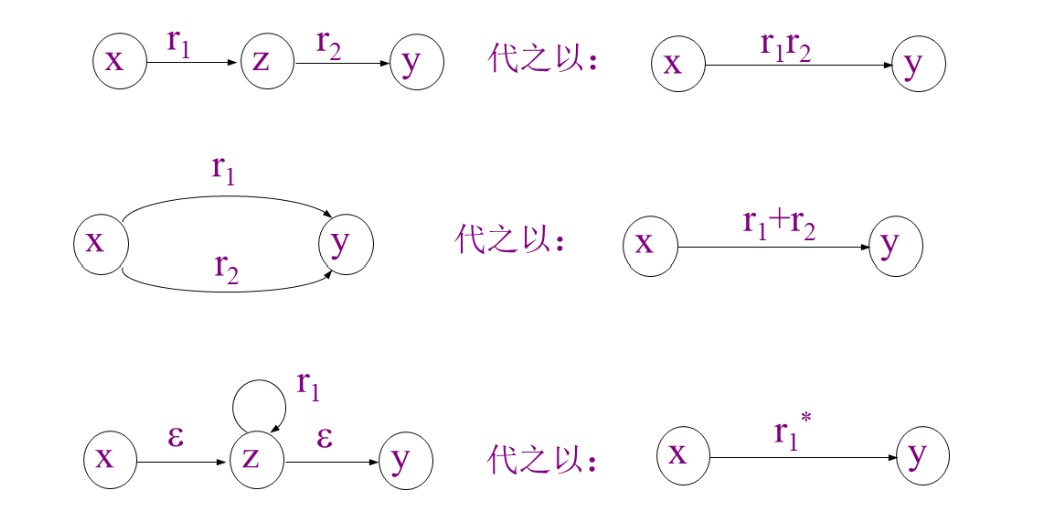
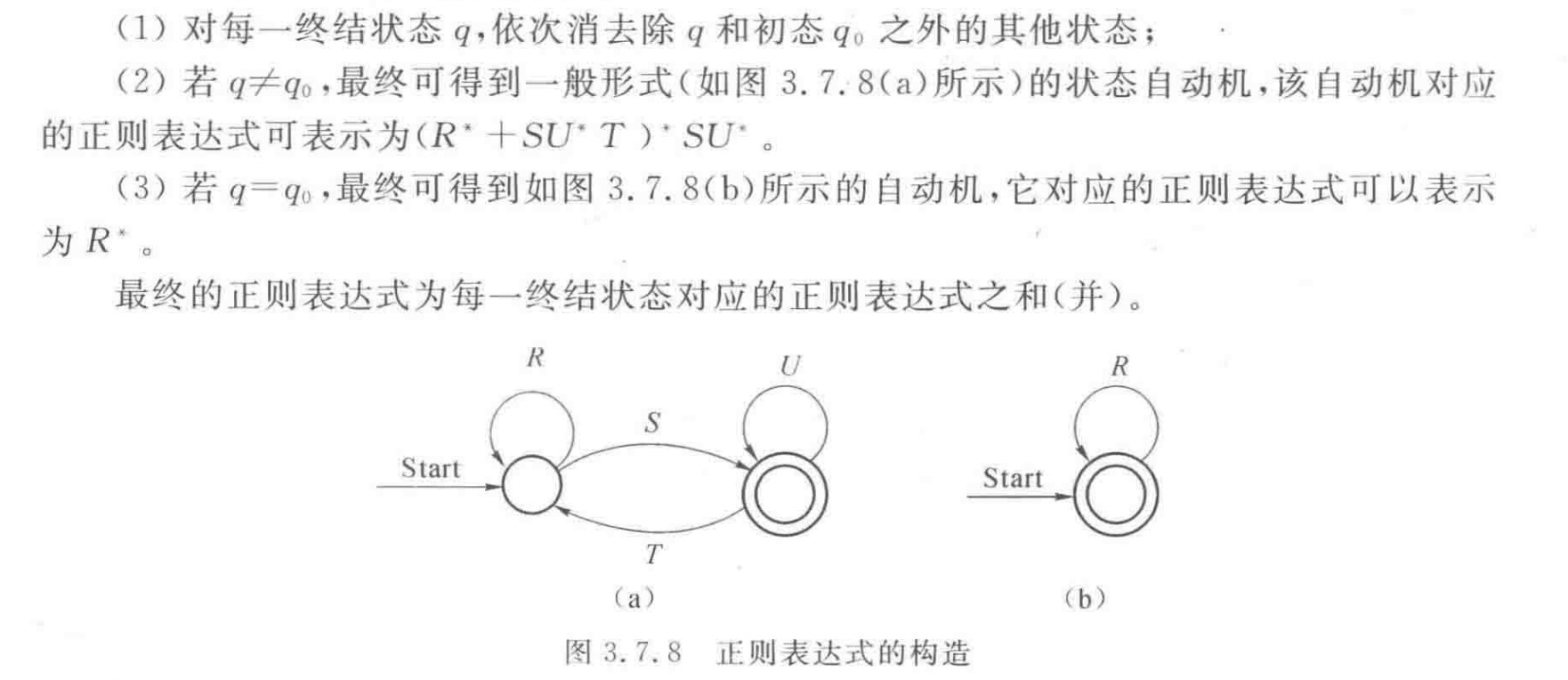
例:
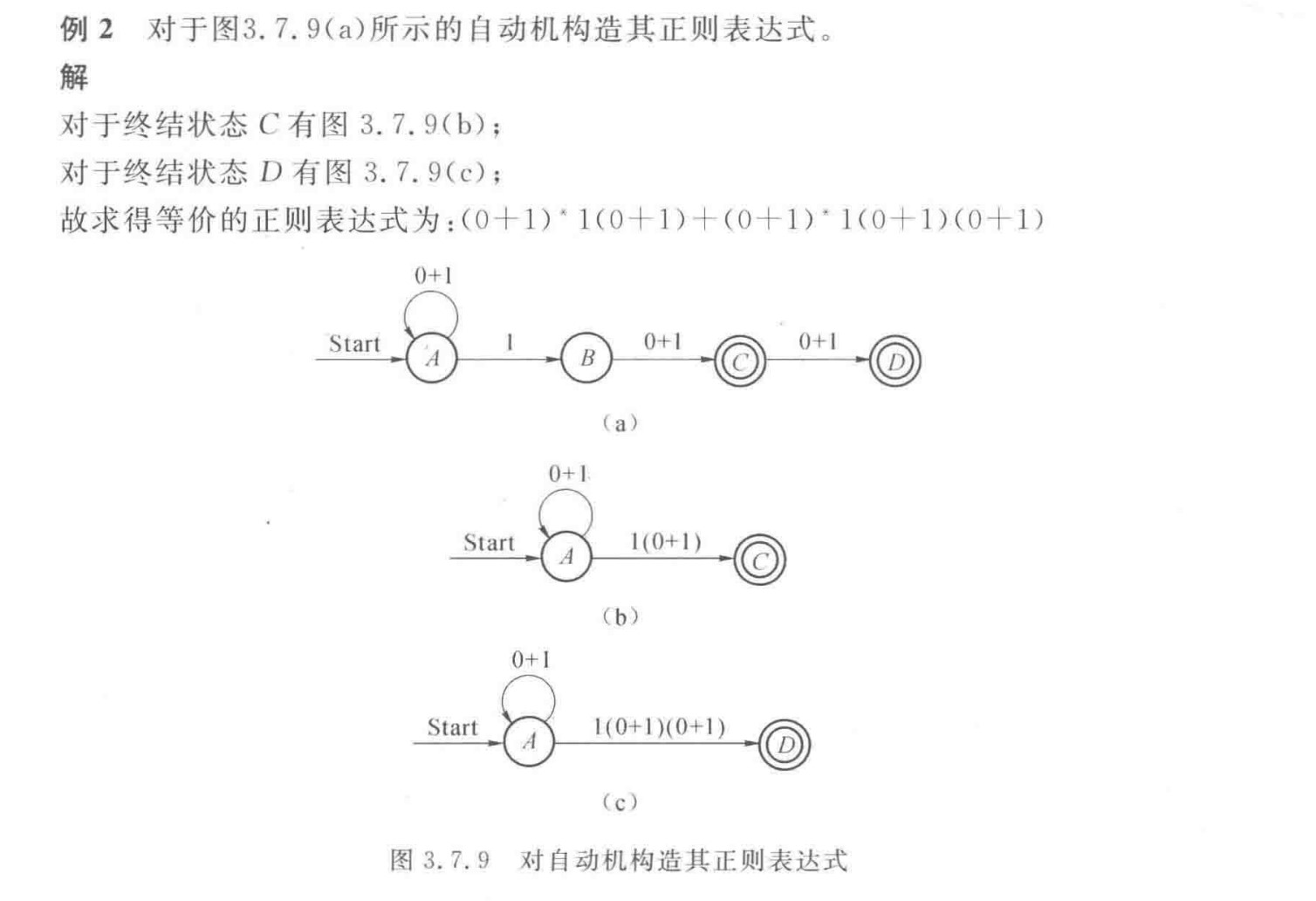
正则表达式构造ε-NFA
归纳构造过程
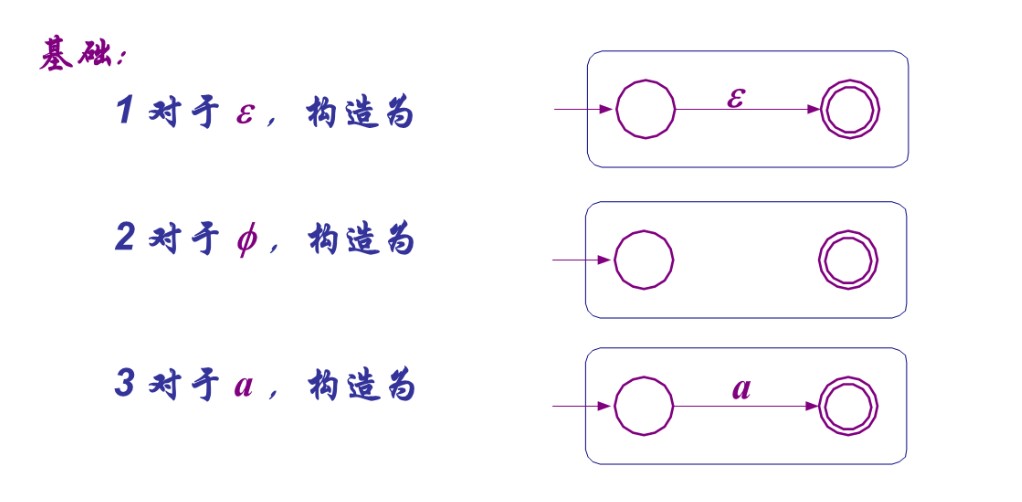
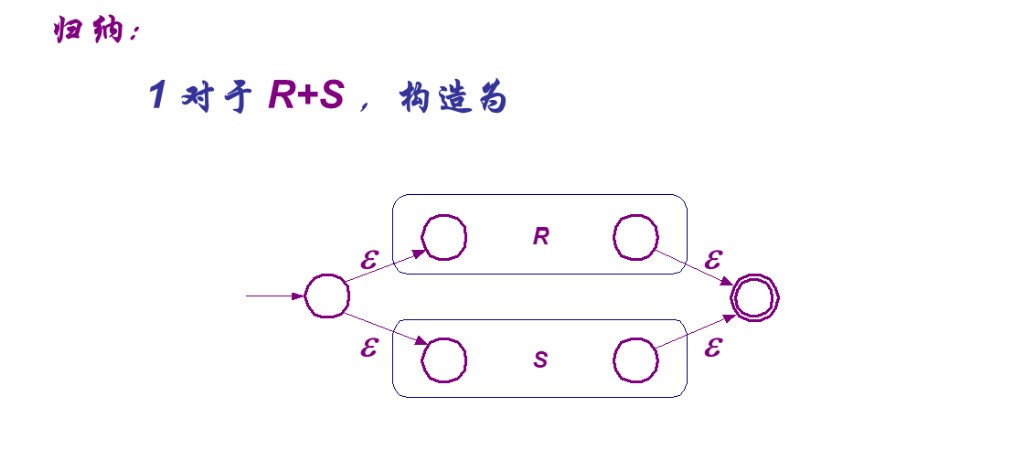
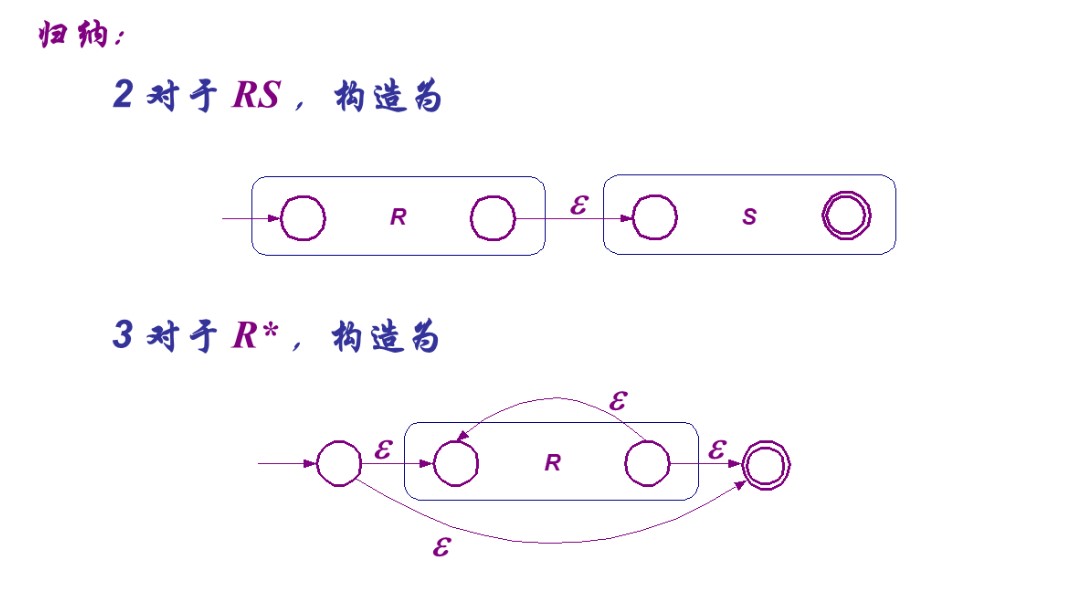
它看起来要麻烦得多,实在不理解那还是背下来吧XD
例:
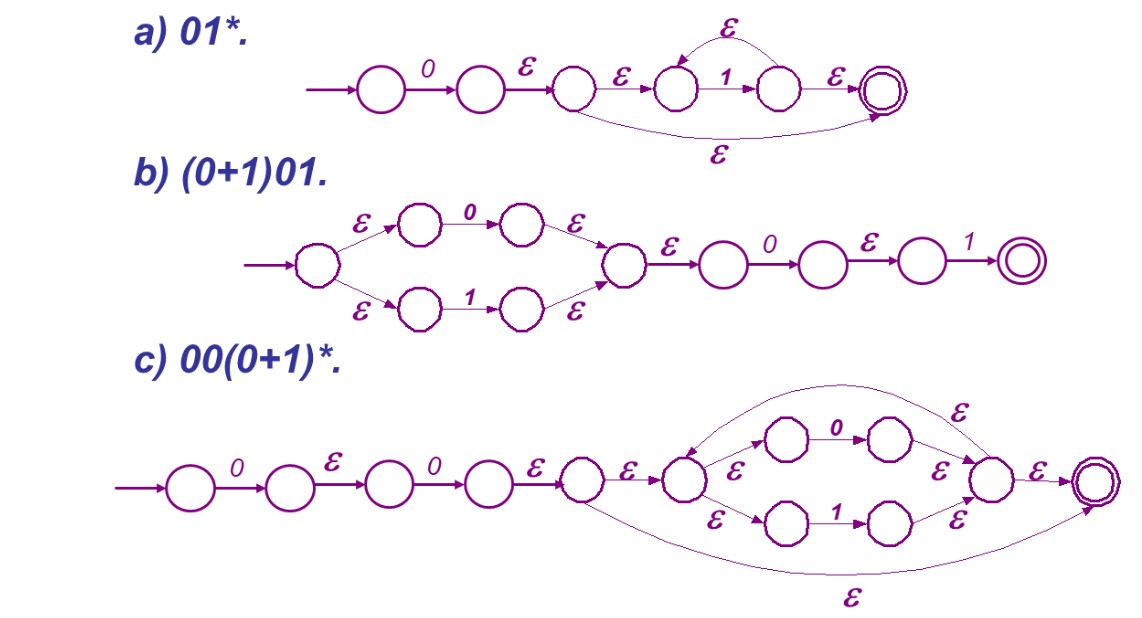
右线性文法与有限自动机
证明看得头疼,让我们来一起记结论吧!
右线性文法转换到有限自动机

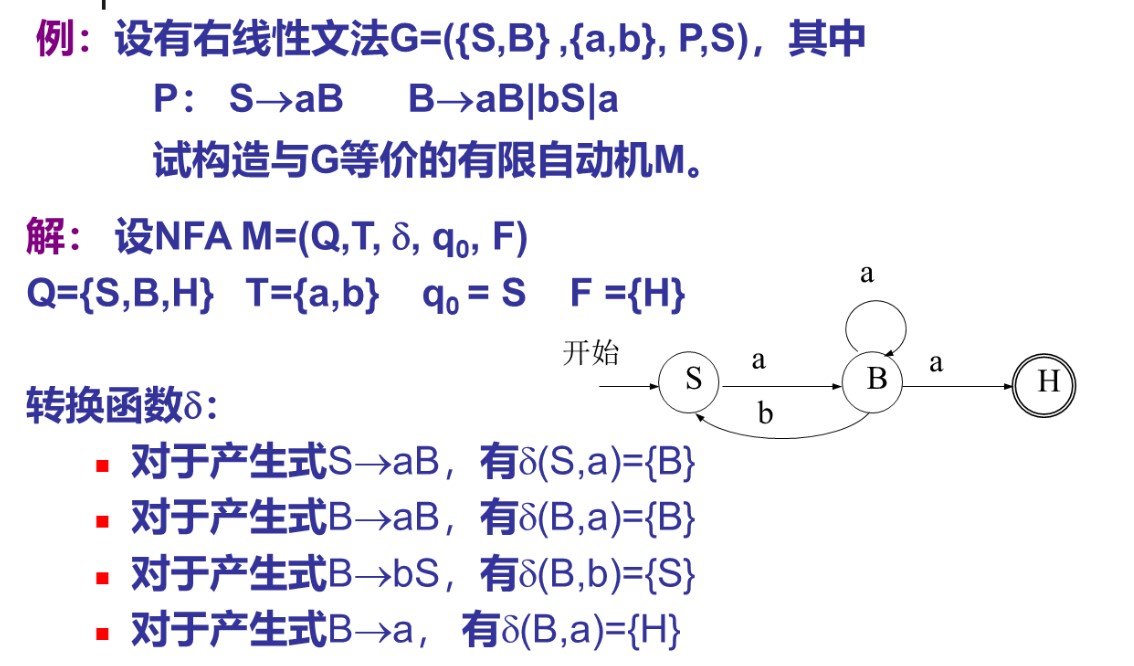
有限自动机转换到右线性文法
 这个构造方法真的很玄妙啊
这个构造方法真的很玄妙啊
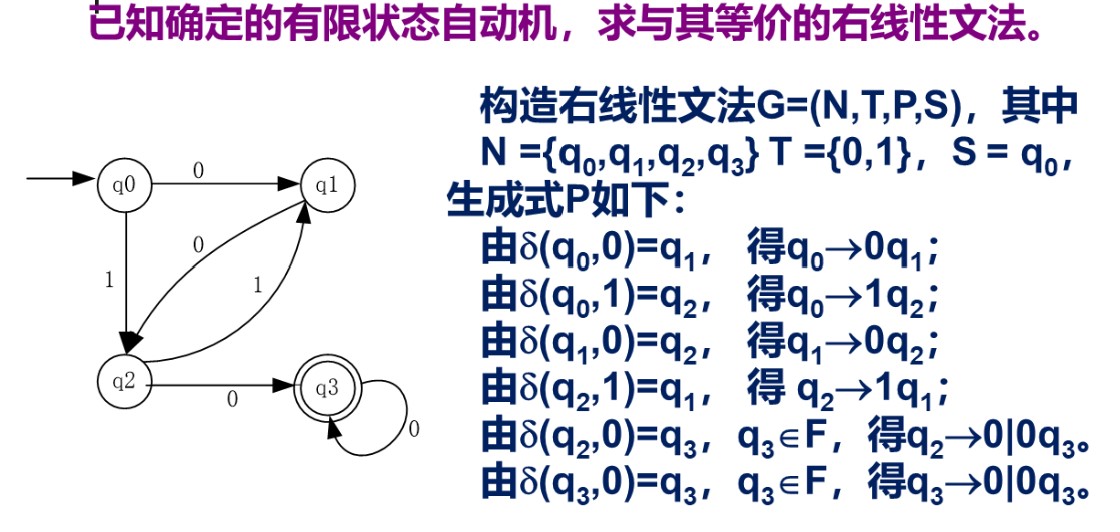
右线性语言的性质
DFA的最小化
最小化:有限自动机M不存在不可达状态和没有互为等价的状态。
把有限自动机的状态集构成划分(两个划分块的状态都可区分,同一划分快中任意两个状态都等价)。
填表法:
- 先删去不可达状态
- 终止状态和非终止状态可区分
- 如果p、q可区分,而r、s通过某个输入符号a可分别转移到p、q,则p、q也可区分
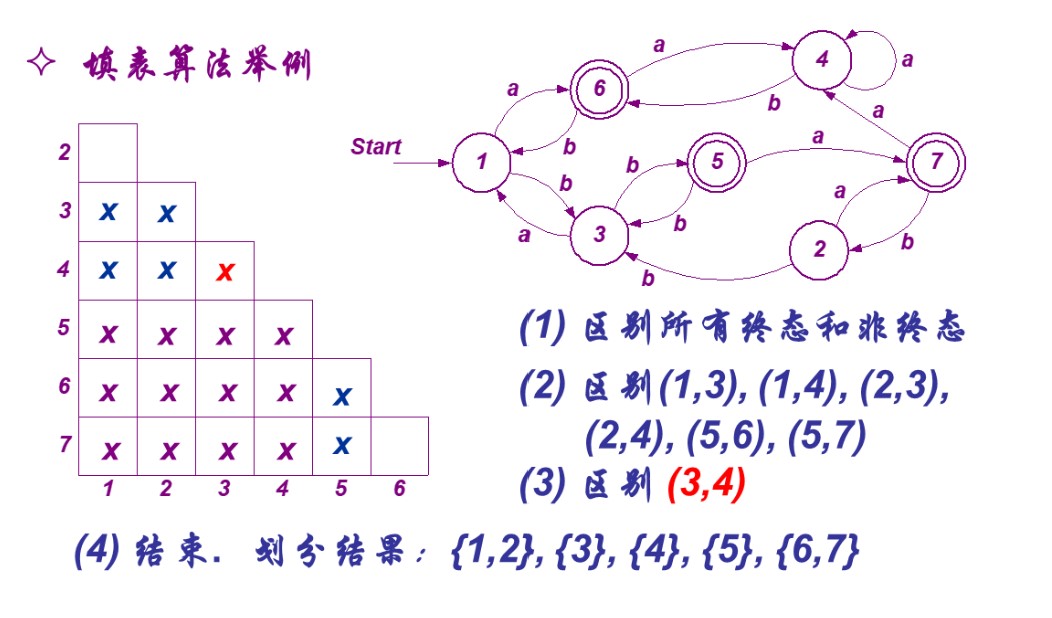
- 因为终止状态和非终止状态可区分,所以把(1, 5)到(1, 7)、(2, 5)到(2, 7)、(3, 5)到(3, 7)、(4, 5)到(4, 7)的格子打上×
- 剩下的格子依次输入字符a或b观察下一状态,比如状态1和状态3接收字符a后分别到达状态6和状态1,而(6 , 1)已经×,所以(1, 3)也要打上×。以此类推。
- 最后会发现只有(1, 2)和(6, 7)没有打上×,则状态1、状态2等价,状态6、状态7等价
- 划分结果为{1, 2}, {3}, {4}, {5}, {6, 7}
- 然后构造DFA
其实最开始觉得它和数电好像好像……而我数电又学得极差(不愿回忆),理解了好久,希望没理解错。
泵浦引理
指路哈工大形式语言与自动机网课,讲得很清楚。

这里用到了鸽巢原理,即 被重复的部分一定非空且在前N个字符中一定出现 。
泵浦引理用来证明一个语言不是正则集,使用反证法。
举个栗子:

也是理解了好久一直搞不明白,最后找了个网课听好像就懂了,做题的话也都是一个套路。
右线性语言的封闭性
设$L_1$、$L_2$、$L$是右线性语言,则$L_1∪L_2$、$L_1L_2$、$L^*$、$\bar{L}$、$L_1∩L_2$、置换都是封闭的
都是证明,很难搞。
双向和有输出的有限自动机
双向有限自动机:读头可以向左或右移的自动机
有输出的有限自动机:米兰机(输出字符与状态和输入字符有关),摩尔机(输出字符仅与状态有关)
上下文无关文法与下推自动机
推导树与二义性
推导树就是画图,很简单。
二义性就是一个表达式能画出两棵推导树。
上下文无关文法的变换
消去ε生成式

如果$S→ε$,则要在最前面添加$S_1→ε|S$
消去无用符号
- 如果从某个非终结符推不出终结符串,则删去该非终结符及其相关产生式。
- 如果某非终结符不出现在起始符S推导的句型中,则删去。
必须先消去非产生的,再消去不可达的。
消去单产生式
直接替换单产生式。
化简顺序:
消除ε生成式→消去单产生式→消去无用符号
消左递归

Chomsky范式和Greibach范式
Chomsky范式
产生式形如$A→BC$、$A→a$
消除ε生成式、消去单产生式、消去无用符号
对生成式$A→D_1D_2…D_n$ $(n≥2)$
若$D_i∈T$,则引入新生成式$B_i→D_i$,$B_i$是新的非终结符
若$D_i∈N$,则令$B_i=D_i$,从而将原生成式变化为$A→B_1B_2…B_n$,当$n≥2$时,再将其转化为$A→B_1C_1$,$C_1→B_2C_2$,……,$C_{n-1}→B_{n-1}B_n$
Greibach范式
产生式形如$A→aβ$
- 2型文法变换为CNF
- 将非终结符排序,进行代换
- 消左递归
- 回代

当时写作业有一道很变态的题,做很久都没做出来……sooooo sad
下推自动机
感觉下推自动机贼麻烦,学的时候没学明白,考前找了点资料生啃下来的。难顶。
下推自动机和上下文无关语言之间的转换很玄学……
上下文无关语言的性质
泵浦引理
封闭性
判定问题
二义性
图灵机
图灵机,你好神奇……我学不懂……